베이즈 정리

3분

확률은 우리의 삶을 지배한다. 우리는 의식하지 않지만 확률을 매일 사용하고 있다. 이 글에서 우리는 확률 분야에서 가장 중요한 정리 중 하나인 베이즈 정리를 논한다.

검토 및 승인: 심리학자 Sergio De Dios González.

마지막 업데이트: 20 5월, 2023

베이즈 정리는 확률의 한 축이다. 이 정리는 18세기에 이 이론을 제안한 토마스 베이즈(1702-1761년)의 이름에서 따왔다. 하지만 그는 정확히 무엇을 설명하려고 했을까? 미리암 웹스터 사전에 따르면 확률이란 기존의 가능한 결과의 총 수에 대해 주어진 사건을 생성하는 것, 동등하게 발생 가능한 결과의 전체 집합에서의 발생한 결과 수의 비율이다.

많은 확률 이론들이 세계를 지배한다. 예를 들어, 당신이 의사에게 갈 때 의사는 치료할 가능성이 가장 높은 것으로 처방한다. 게다가, 광고주들은 자신들이 홍보하는 제품을 더 많이 구매할 가능성이 있는 사람들에게 광고 캠페인을 집중한다. 게다가 당신은 더 적은 시간이 걸릴 가능성이 있는 경로로 매일 통근하는 것을 선택한다.

전체 확률의 법칙

가장 유명한 확률 법칙 중 하나는 전체 확률의 법칙이다. 전체 확률의 법칙이 무엇인지 분석하는 것이 중요하다. 이것을 이해하기 위해서 다음 예를 들어보자.

어떤 나라에서 시민의 39%가 여성이라고 가정해 보자. 우리는 또한 여성의 22%와 남성의 14%가 직업이 없다는 것을 알고 있다. 그렇다면 이 나라의 인구 중에서 무작위로 뽑은 사람이 실업자 P(U)일 확률은 얼마나 될까?

확률 이론에 따르면 이것은 확률을 표현하는 방법이다.

그 사람이 여성일 확률 : P (W)
그 사람이 남성일 확률 : P (M)
시민들의 39 %가 여성이라는 것을 알고 있기 때문에 P (W) = 0.39

따라서 P (M) = 1 – 0.39 = 0.61 이라고 추론 할 수 있다.

또한 명시된 문제는 조건부 확률을 제공한다.

여성이 실업자일 확률 : P (U | W) = 0.22
남성가 실업자일 확률 : P (U | M) = 0.14

따라서 총 확률 법칙을 사용하면 다음과 같은 결과를 얻을 수 있다.

P (U) = P (W) P (U | W) + P (M) P(U | M)

P (U) = 0.22 × 0.39 + 0.14 × 0.61

P (U) = 0.17

따라서 무작위로 선택한 사람이 P(U)라는 실업자일 확률은 0.17이 된다. 결과는 두 조건부 확률(0.14 < 0.17 < 0.22) 사이에 있음을 알 수 있다.

베이즈 정리

이제 당신이 어떤 양식을 작성하기 위해 무작위 성인을 선택했다고 가정해보자. 그리고 당신은 그들이 직업이 없다는 것을 깨달았다. 이 경우, 그리고 앞의 예를 고려해 봤을 때 무작위로 선택한 이 사람이 여성일 확률은 얼마나 될까 [P(W | U)]?

이 문제를 해결하려면 베이즈의 정리를 적용해야 한다. 구체적으로, 당신은 이 사건에 대해 당신이 가지고 있는 이전의 정보를 고려하여 사건의 확률을 계산하기 위해 이 정리를 사용한다. 당신은 사건 A가 그 확률에 영향을 미치는 특정 특성(B)을 충족한다는 것을 알면서 사건 A의 확률을 계산할 수 있다.

이 경우, 우리는 당신이 어떤 양식을 작성하기 위해 무작위로 선택한 사람이 여성일 가능성에 대해 말하고 있다. 그러나, 그 확률은 그 사람이 직업을 가지고 있는지 없는지에 대해 독립적이지 않을 것이다.

베이즈 정리 공식

다른 정리와 마찬가지로 확률도 계산하는 공식이 필요하다.

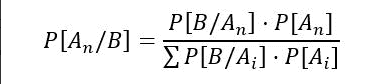
어려워 보이지만 모든 것에는 다음과 같은 설명이 있다.

우선, B는 우리가 사전 정보를 가지고 있는 사건이다.
한편, A(n)라는 용어는 다른 조건부 사건을 가리킨다.
우리는 숫자에 조건부 확률을 가지고 있다. 이것은 다른 사건(B)도 발생한다는 것을 알고 있는 어떤 사건( A)가 발생할 확률을 말한다. 우리는 이것을 P(A | B)로 정의하고 ‘A의 주어진 B의 확률‘로 표현한다.
분모에는 P(B)와 동등한 것을 가지고 있다.

베이즈 정리 예제

앞의 예제로 돌아가서 설문지를 작성하기 위해 무작위 성인을 선택했고 일자리가 없다는 것을 알았다고 가정해보자. 이 사람이 여성일 확률 [P (W | U)]은 얼마인가?

음, 이전의 예를 고려해 볼 때, 우리는 활동 인구의 39%가 여성이라는 것을 알고 있다. 우리는 그 때 나머지가 남자라는 것을 안다. 또 여성 실업률은 22%, 남성 실업률은 14%로 알고 있다.

마지막으로, 우리는 무작위 실업자를 선택할 확률은 0.17이라는 것을 안다. 그래서 베이즈의 정리를 적용하면 우리가 얻을 수 있는 결과는, 모든 실업자 중에서 무작위로 선택한 사람이 여성이 될 확률은 0.5이다.

P (W | U) = (P (W) * P (U | W) / P (U) = (0.22 * 0.39) / 0.17 = 0.5

우리는 확률에 관한 가장 빈번한 혼란 중 하나를 언급함으로써 이 글을 마무리할 것이다. 그것은 오직 0과 1사이의 범위만 가질 수 있다. 어떤 사건의 확률이 0이라면 그것은 반드시 일어날 수 없다. 반면에 만약 그 확률이 1이라면 그것은 반드시 일어날 것이다.